Today we are going to write a bot using Clojure to beat the game 2048. We are going to use a variation of the minimax algorithm called expectimax.

1. game rules
You can merge tiles by merging the whole board either horizontally or vertically. If you manage to get the 2048 tile, you win. After a merge (= player’s turn), a tile will appear randomly on an empty slot. The chance of that tile being a 4 is 0.1, the chance of it being a 2 is 0.9. After reaching the 2048 you can keep playing and the same rules apply.
In fact we are going to write a bot that is able to get the 8192 tile.
2. heuristic
First of all, we need a measure of how well the bot performs. If you want to come up with your own heuristic, pause here and play a few rounds.
After a few rounds, you probably realize that the largest tile should stay in a corner. Intuitively the larger tiles should stick together.
We can formalize these observations by splitting up the heursitic score into two parts:
cluster score
The cluster score is simply the actual board weighted by a matrix:
(def matrix [[15 14 13 12] [11 10 9 8] [7 6 5 4] [3 2 1 0]])(defn cluster-score [board matrix]
(reduce +
(for [x [0 1 2 3]
y [0 1 2 3]]
(* (nth (nth board x) y) (nth (nth matrix x) y)))))This is a measure of how monotone the board is. It leads to the highest tile sticking to the upper-left corner.
heterogeneous score
This score is actually a penalty. The higher this score, the worse for the player. It is calculated by summing the differences of all tiles to all their adjacent neighbours.
(defn neighbour-score
[x y board]
(reduce +
[(Math/abs (- (nth (nth board x) y) (nth (nth board (max (dec x) 0)) y)))
(Math/abs (- (nth (nth board x) y) (nth (nth board (min (inc x) 3)) y)))
(Math/abs (- (nth (nth board x) y) (nth (nth board x) (max (dec y) 0))))
(Math/abs (- (nth (nth board x) y) (nth (nth board x) (min (inc y) 3))))]))
(defn hetero-score
[board]
(reduce +
(for [x [0 1 2 3]
y [0 1 2 3]]
(neighbour-score x y board))))Finally, substract the penalty score from the cluster score:
(defn score
"heuristic score for a given board"
[board]
(- (cluster-score board matrix) (hetero-score board)))And we are left with a function that maps a game board to a score. We are going to implement an algorithm that tries to maximize this score.
3. game simulation
The next part consists of a function to simulate moves. A move is either a player move, or a move by the environment (= spawning tiles). This distinction is important as we will see later on. The function we are looking for has following signature:
(defn execute-move
"returns board after execution of move"
[board move]
next-board)The first observation is, considering only horizontal moves, that each row merges independently. Our second observation reveals, that vertical moves can easily be transformed to horizontal moves by transposing the board. The last observation shows, that a left-merge equals a right-merge of the reversed vector.
If we solve merging of a single row along a single axis, we solve simulating player moves:
(def moves {:up 0 :down 1 :left 2 :right 3})
(defn remove-zeroes
[row]
(vec (filter (complement zero?) row)))
(defn pad-zeroes
"right pads zeroes to length 4"
[row]
(loop [row row]
(if (>= (count row) 4)
row
(recur (conj row 0)))))
(defn merge-pair
"merges two elemnts of a row to the left, considering the original row"
[row a b original]
(if (and (= (nth row a) (nth row b))
(or (nil? original) (= (nth original 2) (nth row 2))))
(-> row
(assoc a (+ (nth row a) (nth row b)))
(assoc b 0))
row))
(defn merge-row-left
[row]
(-> row
(remove-zeroes)
(pad-zeroes)
(merge-pair 0 1 nil)
(merge-pair 2 3 nil)
(merge-pair 1 2 row)
(remove-zeroes)
(pad-zeroes)))
(def m-left (memoize merge-row-left))It is noteworthy, that we memoize the function merge-row-left. Assuming the maximum tile we want to reach is 8192 (= 2^13), there are only 13^4 possible combinations to make up a row. This function will potentially be called millions of times per second while searching for the score maximizing player move.
Introducing some transpose functions leads to our goal function execute-move:
(defn- merge-row-right
[row]
(-> row
(reverse)
(m-left)
(#(vec (reverse %)))))
(def m-right (memoize merge-row-right))
(defn- merge-row
[move]
(if (= move :right)
m-right
m-left))
(defn- merge-rows
[board move]
(map (merge-row move) board))
(defn- transpose-move
[move]
(cond
(= move :down) :right
(= move :up) :left))
(defn- transpose
[board]
(apply mapv vector board))
(defn execute-move
[board move]
(if (> 2 (get moves move))
(transpose (merge-rows (transpose board) (transpose-move move)))
(merge-rows board move)))4. expectimax
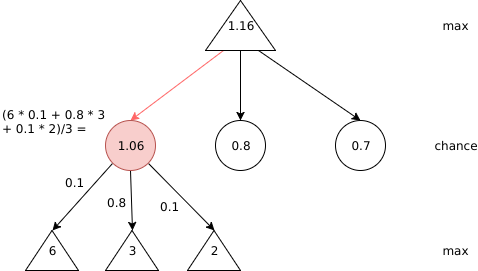
We are using a search algorithm with an adaptive depth of search. While searching the bot alternates between the chance layer and the max layer. The chance layer is where the environment spawns a tile randomly. We don’t know where it’s going to happen and we don’t know what tile it’s going to be: We have to calculate using the expectancy value of all possible boards:
(defn- average
[numbers]
(/ (apply + numbers) (count numbers)))
(defn- all-spawns
"returns a list of boards by spawning tiles of `kind` on all free slots"
[board kind]
(->>
(for [x [0 1 2 3]
y [0 1 2 3]]
(if (= (nth (nth board x) y) 0)
(assoc-in (vec board) [x y] kind)))
(filter (complement nil?))))
(defn calculate-chance
"returns heuristic score of current chance node"
([board depth limit original]
(if (= board original)
0
(calculate-chance board depth limit)))
([board depth limit]
(if (or (= depth limit))
(ai/m-score board)
(average (concat
(map #(* (calculate-max % (inc depth) limit) 0.9) (all-spawns board 2))
(map #(* (calculate-max % (inc depth) limit) 0.1) (all-spawns board 4)))))))At the max layer on the other hand, we are in control. We can simply execute all possible moves given a board and return the highest heuristic score using calculate-max.
(defn- all-moves
"returns a list of all possible moves given a board"
[board]
(filter #(not= % board) (map #(game/execute-move board %) ai/moves)))
(defn calculate-max
"returns heuristic score of current max node by returning the max value of the children"
([board depth limit original]
(if (= board original)
0
(calculate-max board depth limit)))
([board depth limit]
(if (or (= depth limit) )
(ai/m-score board)
(apply max (concat (map #(calculate-chance % (inc depth) limit) (all-moves board)) '(0))))))
Lastly, we expose our magnificent AI through a single function best-move returning the best move given a board:
(defn-n count-zeroes
"amount of empty slots on a board"
[board]
(or (-> board
(flatten)
(frequencies)
(get 0)) 0))
(defn-n decide-depth
"set depth of search according to amount of empty slots left"
[number]
(cond
(> number 12) 1
(> number 7) 2
(> number 4) 3
(> number 1) 4
(>= number 0) 6
:else 2))
(defn- get-depth
"returns depth of search for current board"
[board]
(-> board
(count-zeroes)
(decide-depth)))
(defn best-move
"returns best move for a board"
[board]
(let [moveh (sort-by val > (into (sorted-map)
(pmap
(fn [x] {x (ex/calculate-chance (game/execute-move board x) 0 (get-depth board) board)}) moves)))]
(get moves-map
(first (keys moveh)))))
(def m-best-move (memoize best-move))Using pmap I am able to get 100% CPU usage on Java 8 HotSpot VM and a dual core machine. At most there are only 4 functions getting executed in parallel, so the performance gain through parallelization is probably not that great on machines with more cores.
You can find the source in this repo.


